عدد ۲۴ مضرب چه اعدادی است؟ پاسخ لینک زیر 👇
عدد ۳۶ مضرب چه اعدادی است؟ پاسخ لینک زیر 👇
عدد ۴۸ مضرب چه اعدادی است؟ پاسخ لینک زیر 👇
در این کاربرگ
اعداد مثلثی را با استفاده از شکل معرفی میکنیم
دوم اینکه اگر یک عدد مثلثی را به ما داده باشند بدون استفاده از فرمول عدد مثلثی بعدی را پیدا کنیم
فرمول اعداد مثلثی را پیدا میکنیم
اعداد مثلثی را با استفاده از فرمول به دست میآوریم
در این پست یاد می گیریم چگونه رابطه الگو را پیدا کنیم
پاسخنامه 👇
نکته مهم :
با تقریب کمتر از ۱۰ با تقریب دهگان یکی است
در سوالات با تقریب کمتر از ۱۰۰ همان با تقریب صدگان است.
با تقریب یک همان تقریب کمتر از یکان است
نکته: اگر در سوال گفته بود با تقریب رقم صدم و یا نوشته بود با تقریب کمتر از ۰⁄۰۱ یعنی رقمهایی که در مرتبه هزارم و ۱۰ هزارم و الی آخر هستند را با صفر جایگزین کنید.
در روش قطع کردن
ابتدا ارزش مکانی تقریب را مشخص میکنیم و زیر آن خط میکشیم
از سمت چپ رقمهای عدد را مینویسیم تا به رقمی که زیر آن خط کشیدیم برسیم و در پایان عددهای سمت راست آن را با صفر جایگزین میکنیم .

قبل ازدیدن ویدیوی تبدیل کسر به درصد حتما سوالات را دانلود کرده و حل کنید
دانلود سوالات تبدیل کسر به درصد ساده تا پیشرفته
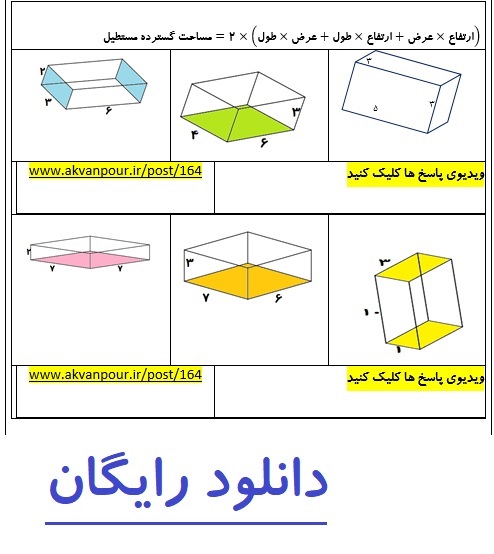
برای تسلط بر فرمول بالا کاربرگ زیر را حل کنید
دانلود کاربرگ مساحت گسترده مکعب مستطیل
برای دیدن ویدیو روی تصویر کلیک کنید
برای دیدن ویدیو روی تصویر کلیک کنید

برای تسلط بر فرمول بالا کاربرگ زیر را حل کنید
برای دیدن ویدیو روی تصویر کلیک کنید
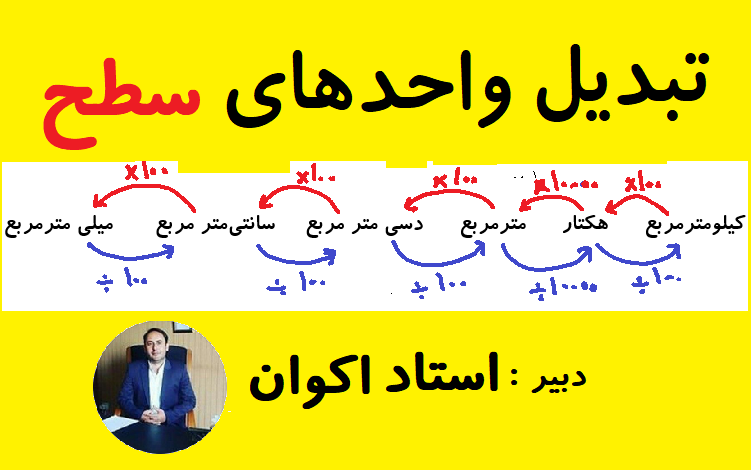
اندازه گیری
همه فرمولهای هندسی ریاضی دبستان در یک عکس:
تعداد پاره خط ها و نیم خط ها
1-هرگاه چند نقطه ی متمایز(جدا از هم)،بر روی یک خط راست باشند تعداد پاره خط ها از فرمول زیر به دست می آید.
2 ÷ (تعداد فاصله ها × تعداد نقطه ها ) = تعداد پاره خط ها
توجه : تعداد فاصله ها همیشه یکی کمتر از تعداد نقطه ها است.
2- هرگاه چند نقطه ی متمایز،بر روی خط راست باشند، تعداد نیم خطها از فرمول زیر،به دست می آید.
2 × تعداد نقطه ها = تعداد نیم خطها
3- هرگاه چند نقطه ی متمایز، برروی یک نیم خط باشند،تعداد نیم خطها مانند مثال زیر به دست میآید.
مثال: برروی یک نیم خط،هفت نقطه ی متمایز وجود دارد چند نیم خط، در شکل وجود دارد؟
پس (8 = 1 + 7 ) نقطه داریم یعنی 8 نیم خط خواهیم داشت.
4- هرگاه چند نقطه ی متمایز، برروی یک پاره خط باشند نیم خطی، درشکل وجود ندارد.
برش و قسمت:
وقتی می خواهیم یک قطعه یا جسمی رشته مانند را به قسمت های مساوی ویا نامساوی تقسیم کنیم همیشه تعداد قسمتها یکی بیشتر از تعداد برشها است.
مثال: یک آهنگر , میله ای به طول 12 متر را به چهار قسمت تقسیم کرد او برای این کار چند برش زده است؟
برش 3 = 1 – 4 (قسمت)
مثال: زاویه ای که دو عقربه ی ساعت شمار و دقیقه شمار در ساعت 1:50 می سازند چند درجه است؟
زاویه ی بین دو عقربه
مجموع زوایای داخلی چند ضلعی ها:
برای این که مجموع زاویه های داخلی هر چند ضلعی رامحاسبه کنیم ، تعداد ضلع ها را منهای 2 نموده ، در 180 ضرب می کنیم.
180 × (2 – تعداد ضلع ها ) = مجموع زاویه های داخلی
مثال : مجموع زاویه های داخلی یک 5 ضلعی را به دست آورید؟
درجه 540 = 180× (2 – 5 ) : پنج ضلعی
تعداد قطرهای چندضلعی ها:
از تعداد ضلع ها، 3 تا کم کرده، جواب را در تعداد ضلع ها ضرب کرده و سپس جواب را بر 2 تقسیم می کنیم.
2÷ تعداد ضلع ها × ( 3 - تعداد ضلع ها ) = تعداد قطرها
از هر راس چند ضلعی به اندازهی (3- تعدا ضلع ها ) قطر می گذرد. مثلا از یک راس چهار ضلعی ( 1= 3 – 4) یک قطر می گذرد.
مثال : یک شش ضلعی چند قطر دارد؟
تعداد قطرها 9= 2 ÷ 6 × ( 3 – 6 )
تعداد زاویه ها:
هرگاه در چند زاویه ی مجاور که دارای راس مشترک هستند ، بخواهیم تعداد زاویه ها را تعیین کنیم ، از فرمول زیر استفاده می کنیم.
2 ÷ (تعداد فاصله ها× تعداد نیم خط ها ) = تعداد زاویه ها
توجه : تعداد فاصله ها،از تعداد نیم خط ها یکی کم تر است.
مثال : در شکل روبرو چند زاویه وجود دارد؟
ارتفاع وارد بر وتر:
برای محاسبه ارتفاع وارد بر وتر ، می توانیم از فرمول زیر استفاده کنیم.
وتر ÷ حاصل ضرب دو ضلع زاویه ی قائمه= ارتفاع وارد بر وتر
مثال : اگر دو ضلع زاویهی قائمه مثلث قائم الزاویهای 5 و 12 س باشد و وتر آن 15 س باشد. طول ارتفاع وارد بر وتر آن چقدر است؟
قانون سه زاویه:برای رسم یک مثلث به روش سه زاویه باید بدانیم که زوایایی که میتوان با آنها یک مثلث رسم کرد باید حتما از یک قانون تبعیت کنند. باید مجموع سه زاویه 180 درجه شود. برای مثال:
| 50 درجه، 70 درجه، 60 درجه | 60 +70 +50 = 180 | درست |
| 50 درجه، 70 درجه، 70 درجه | 70 +70 +50 = 190 | نادرست |
| 50 درجه، 70 درجه، 50 درجه | 50 +70 +50 = 170 | نادرست |
آیا سه ضلعی منتظم یا همان متساوی الاضلاع تقارن چرخشی دارد؟ چند درجه باید بچرخانیم؟
آیا چهار ضلعی منتظم یا همان مربع تقارن چرخشی دارد؟ چند درجه باید بچرخانیم؟
آیا پنج ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید بچرخانیم تا شکل روی خودش قرار بگیرد؟
آیا پنج ضلعی منتظم تقارن مرکزی دارد؟
آیا شش ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید بچرخانیم تا شکل روی خودش قرار بگیرد؟
آیا شش ضلعی منتظم تقارن مرکزی دارد؟
آیا هشت ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید بچرخانیم تا شکل روی خودش قرار بگیرد؟
آیا هشت ضلعی منتظم تقارن مرکزی دارد؟
آیا نه ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید شکل را بچرخانیم تا روی خودش قرار بگیرد؟
آیا نه ضلعی منتظم تقارن مرکزی دارد؟
در حالت کلی کدام یک از چند ضلعیهای منتظم تقارن چرخشی
با درجه چرخش طبیعی دارند؟
نکته های تقارن محوری
نکته های تقارن مرکزی
- نکته های تقارن چرخشی
الف) نکته های تقارن محوری
محور تقارن چیست؟ با یک مثال توضیح دهید
مثلث مختلف الاضلاع چند محور تقارن دارد؟
مثلث متساوی الساقین چند محور تقارن دارد؟ آنها را رسم کنید
مثلث متساوی الاضلاع چند محور تقارن دارد؟ آنها را رسم کنید
مثلث قایم الزاویه چند محور تقارن دارد؟ آنها را رسم کنید
مثلث قایم الزاویه متساوی الساقین چند محور تقارن دارد؟ آنها را رسم کنید
مربع چند محور تقارن دارد؟ آنها را رسم کنید
مستطیل چند محور تقارن دارد؟ آنها را رسم کنید
لوزی چند محور تقارن دارد؟ آنها را رسم کنید
متوازی الاضلاع چند محور تقارن دارد؟ آنها را رسم کنید
ذوزنقه چند محور تقارن دارد؟ آنها را رسم کنید
ذوزنقه قائم الزاویه چند محور تقارن دارد؟ آنها را رسم کنید
ذوزنقه متساوی الساقین چند محور تقارن دارد؟ آنها را رسم کنید
کایت یا بادبادک چند محور تقارن دارد؟ آنها را رسم کنید
چهار ضلعی مختلف الاضلاع چند محور تقارن دارد؟ آنها را رسم کنید
دایره چند محور تقارن دارد؟ آنها را رسم کنید
نیم دایره چند محور تقارن دارد؟ آنها را رسم کنید
ربع دایره چند محور تقارن دارد؟ آنها را رسم کنید
بیضی چند محور تقارن دارد؟ آنها را رسم کنید
ب) نکته های تقارن مرکزی
مرکز تقارن نقطهای است که اگر قرینه شکل را نسبت به آن نقطه دقیقاً بر شکل منطبق میشود
یا نقطهای است که اگر شکل را ۱۸۰ درجه حول آن دوران دهیم شکل دوران یافته بر شکل اول منطبق میشود.
نکته مرکز تقارن نقطهای است که اگر قرینه هر نقطه روی محیط شکل را نسبت به آن نقطه روی محیط شکل قرار میگیرد.
تشخیص مرکز تقارن با خط کش: برای اینکه مشخص شود یک نقطه، مرکز تقارن شکل است یا نه، از هر نقطه روی محیط شکل به نقطه ی داده شده وصل کنیم و به همان
اندازه ادامه دهیم. اگر نقطه ی حاصل روی محیط شکل قرار گرفت، نقطه ی داده شده مرکز تقارن می باشد در غیر این صورت مرکز تقارن نیست.
اگر قرینه شکلی نسبت به یک نقطه روی خود شکل قرار بگیرد به آن نقطه مرکز تقارن شکل میگوییم اگر شکلی مرکز تقارن داشته باشد میگوییم آن شکل تقارن مرکزی دارد.
تقارن مرکزی چیست؟
آیا مثلث تقارن مرکزی دارد؟
آیا مستطیل تقارن مرکزی دارد؟
آیا متوازی الاضلاع تقارن مرکزی دارد؟
آیا ذوزنقه تقارن مرکزی دارد؟
ج) نکته های تقارن چرخشی
آیا سه ضلعی منتظم یا همان متساوی الاضلاع تقارن چرخشی دارد؟ چند درجه باید بچرخانیم؟
آیا چهار ضلعی منتظم یا همان مربع تقارن چرخشی دارد؟ چند درجه باید بچرخانیم؟
آیا پنج ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید بچرخانیم تا شکل روی خودش قرار بگیرد؟
آیا پنج ضلعی منتظم تقارن مرکزی دارد؟
آیا شش ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید بچرخانیم تا شکل روی خودش قرار بگیرد؟
آیا شش ضلعی منتظم تقارن مرکزی دارد؟
آیا هشت ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید بچرخانیم تا شکل روی خودش قرار بگیرد؟
آیا هشت ضلعی منتظم تقارن مرکزی دارد؟
آیا نه ضلعی منتظم تقارن چرخشی دارد؟
چند درجه باید شکل را بچرخانیم تا روی خودش قرار بگیرد؟
آیا نه ضلعی منتظم تقارن مرکزی دارد؟
در حالت کلی کدام یک از چند ضلعیهای منتظم تقارن چرخشی
با درجه چرخش طبیعی دارند؟
آیا مثلث متساوی الاضلاع تقارن چرخشی دارد در این پست به این سوال پاسخ میدهیم.
می خواهیم ببینیم آیا میتوان مثلث متساوی الاضلاع را ۱۸۰ درجه یا کمتر دوران دهیم و روی خودش بیفتد؟



























 لطفا صبر کنید ...
لطفا صبر کنید ...


